98. 验证二叉搜索树

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

 

示例 1：

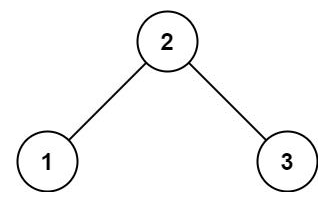
输入：root = [2,1,3]
输出：true

示例 2：

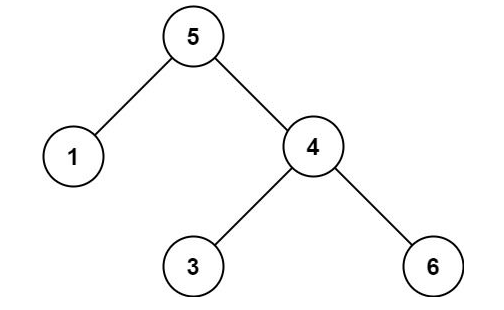
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

 

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

方法一：递归

我们可以对二叉树进行递归中序遍历，如果遍历到的结果是严格升序的，那么这棵树就是一个二叉搜索树。

因此，我们使用一个变量 $\mathit{\text{prev}}$ 来保存上一个遍历到的节点，初始时 $\mathit{\text{prev}}=-\mathrm{\infty }$，然后我们递归遍历左子树，如果左子树不是二叉搜索树，直接返回 $\mathit{\text{False}}$，否则判断当前节点的值是否大于 $\mathit{\text{prev}}$，如果不是，返回 $\mathit{\text{False}}$，否则更新 $\mathit{\text{prev}}$ 为当前节点的值，然后递归遍历右子树。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点个数。

Java

class Solution {
    private TreeNode prev;

    public boolean isValidBST(TreeNode root) {
        return dfs(root);
    }

    private boolean dfs(TreeNode root) {
        if (root == null) {
            return true;
        }
        if (!dfs(root.left)) {
            return false;
        }
        if (prev != null && prev.val >= root.val) {
            return false;
        }
        prev = root;
        return dfs(root.right);
    }
}

C++

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        TreeNode* prev = nullptr;
        function<bool(TreeNode*)> dfs = [&](TreeNode* root) {
            if (!root) {
                return true;
            }
            if (!dfs(root->left)) {
                return false;
            }
            if (prev && prev->val >= root->val) {
                return false;
            }
            prev = root;
            return dfs(root->right);
        };
        return dfs(root);
    }
};

TypeScript

function isValidBST(root: TreeNode | null): boolean {
    let prev: TreeNode | null = null;
    const dfs = (root: TreeNode | null): boolean => {
        if (!root) {
            return true;
        }
        if (!dfs(root.left)) {
            return false;
        }
        if (prev && prev.val >= root.val) {
            return false;
        }
        prev = root;
        return dfs(root.right);
    };
    return dfs(root);
}

Python

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        def dfs(root: Optional[TreeNode]) -> bool:
            if root is None:
                return True
            if not dfs(root.left):
                return False
            nonlocal prev
            if prev >= root.val:
                return False
            prev = root.val
            return dfs(root.right)

        prev = -inf
        return dfs(root)