124. 二叉树中的最大路径和

题目描述

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

 

示例 1：

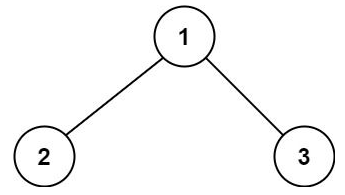
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

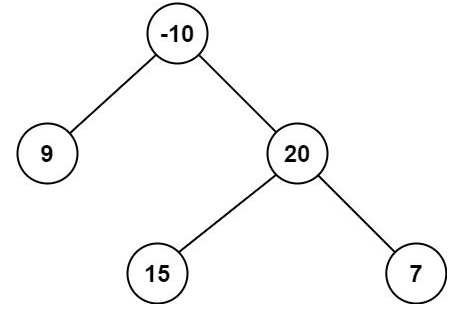
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

 

提示：

• 树中节点数目范围是 [1, 3 * 104]
• -1000 <= Node.val <= 1000

方法一：递归

我们思考二叉树递归问题的经典套路：

1. 终止条件（何时终止递归）
2. 递归处理左右子树
3. 合并左右子树的计算结果

对于本题，我们设计一个函数 $dfs(root)$，它返回以 $root$ 为根节点的二叉树的最大路径和。

函数 $dfs(root)$ 的执行逻辑如下：

如果 $root$ 不存在，那么 $dfs(root)$ 返回 $0$；

否则，我们递归计算 $root$ 的左子树和右子树的最大路径和，分别记为 $left$ 和 $right$。如果 $left$ 小于 $0$，那么我们将其置为 $0$，同理，如果 $right$ 小于 $0$，那么我们将其置为 $0$。

然后，我们用 $root.val+left+right$ 更新答案。最后，函数返回 $root.val+max(left,right)$。

在主函数中，我们调用 $dfs(root)$，即可得到每个节点的最大路径和，其中的最大值即为答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

Java

class Solution {
    private int ans = -1001;

    public int maxPathSum(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = Math.max(0, dfs(root.left));
        int right = Math.max(0, dfs(root.right));
        ans = Math.max(ans, root.val + left + right);
        return root.val + Math.max(left, right);
    }
}

C++

class Solution {
public:
    int maxPathSum(TreeNode* root) {
        int ans = -1001;
        function<int(TreeNode*)> dfs = [&](TreeNode* root) {
            if (!root) {
                return 0;
            }
            int left = max(0, dfs(root->left));
            int right = max(0, dfs(root->right));
            ans = max(ans, left + right + root->val);
            return root->val + max(left, right);
        };
        dfs(root);
        return ans;
    }
};

Python

class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode]) -> int:
            if root is None:
                return 0
            left = max(0, dfs(root.left))
            right = max(0, dfs(root.right))
            nonlocal ans
            ans = max(ans, root.val + left + right)
            return root.val + max(left, right)

        ans = -inf
        dfs(root)
        return ans

TypeScript

function maxPathSum(root: TreeNode | null): number {
    let ans = -1001;
    const dfs = (root: TreeNode | null): number => {
        if (!root) {
            return 0;
        }
        const left = Math.max(0, dfs(root.left));
        const right = Math.max(0, dfs(root.right));
        ans = Math.max(ans, left + right + root.val);
        return Math.max(left, right) + root.val;
    };
    dfs(root);
    return ans;
}