110. 平衡二叉树

给定一个二叉树，判断它是否是 平衡二叉树  

 

示例 1：

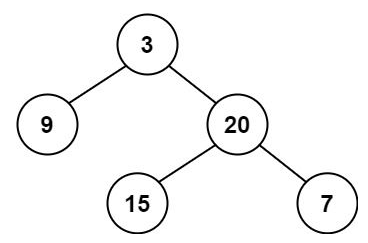
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

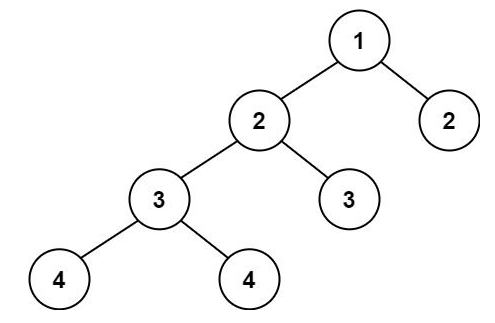
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

 

提示：

• 树中的节点数在范围 [0, 5000] 内
• -104 <= Node.val <= 104

方法一：自底向上的递归

定义函数 $height(root)$ 计算二叉树的高度，处理逻辑如下：

• 如果二叉树 $root$ 为空，返回 $0$。
• 否则，递归计算左右子树的高度，分别为 $l$ 和 $r$。如果 $l$ 或 $r$ 为 $-1$，或者 $l$ 和 $r$ 的差的绝对值大于 $1$，则返回 $-1$，否则返回 $max(l,r)+1$。

那么，如果函数 $height(root)$ 返回的是 $-1$，则说明二叉树 $root$ 不是平衡二叉树，否则是平衡二叉树。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

Java

class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) >= 0;
    }

    private int height(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int l = height(root.left);
        int r = height(root.right);
        if (l == -1 || r == -1 || Math.abs(l - r) > 1) {
            return -1;
        }
        return 1 + Math.max(l, r);
    }
}

C++

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        function<int(TreeNode*)> height = [&](TreeNode* root) {
            if (!root) {
                return 0;
            }
            int l = height(root->left);
            int r = height(root->right);
            if (l == -1 || r == -1 || abs(l - r) > 1) {
                return -1;
            }
            return 1 + max(l, r);
        };
        return height(root) >= 0;
    }
};

TypeScript

function isBalanced(root: TreeNode | null): boolean {
    const dfs = (root: TreeNode | null) => {
        if (root == null) {
            return 0;
        }
        const left = dfs(root.left);
        const right = dfs(root.right);
        if (left === -1 || right === -1 || Math.abs(left - right) > 1) {
            return -1;
        }
        return 1 + Math.max(left, right);
    };
    return dfs(root) > -1;
}

Python

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        def height(root):
            if root is None:
                return 0
            l, r = height(root.left), height(root.right)
            if l == -1 or r == -1 or abs(l - r) > 1:
                return -1
            return 1 + max(l, r)

        return height(root) >= 0