105. 从前序与中序遍历序列构造二叉树

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

 

示例 1:

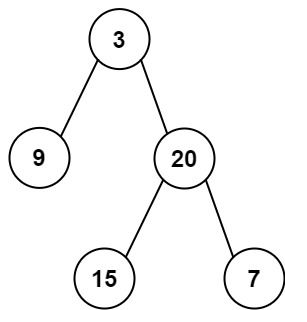
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

 

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

方法一：哈希表 + 递归

前序序列的第一个节点 $preorder[0]$ 为根节点，我们在中序序列中找到根节点的位置 $k$，可以将中序序列划分为左子树 $inorder[0..k]$ 、右子树 $inorder[k+1..]$。

通过左右子树的区间，可以计算出左、右子树节点的个数，假设为 $a$ 和 $b$。然后在前序节点中，从根节点往后的 $a$ 个节点为左子树，再往后的 $b$ 个节点为右子树。

因此，我们设计一个函数 $dfs(i,j,n)$，其中 $i$ 和 $j$ 分别表示前序序列和中序序列的起始位置，而 $n$ 表示节点个数。函数的返回值是以 $preorder[i..i+n-1]$ 为前序序列，以 $inorder[j..j+n-1]$ 为中序序列构造出的二叉树。

函数 $dfs(i,j,n)$ 的执行过程如下：

• 如果 $n\le 0$，说明没有节点，返回空节点。
• 取出前序序列的第一个节点 $v=preorder[i]$ 作为根节点，然后利用哈希表 $d$ 找到根节点在中序序列中的位置 $k$，那么左子树的节点个数为 $k-j$，右子树的节点个数为 $n-k+j-1$。
• 递归构造左子树 $l=dfs(i+1,j,k-j)$ 和右子树 $r=dfs(i+1+k-j,k+1,n-k+j-1)$。
• 最后返回以 $v$ 为根节点且左右子树分别为 $l$ 和 $r$ 的二叉树。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为二叉树节点个数。

Java

class Solution {
    private int[] preorder;
    private Map<Integer, Integer> d = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        this.preorder = preorder;
        for (int i = 0; i < n; ++i) {
            d.put(inorder[i], i);
        }
        return dfs(0, 0, n);
    }

    private TreeNode dfs(int i, int j, int n) {
        if (n <= 0) {
            return null;
        }
        int v = preorder[i];
        int k = d.get(v);
        TreeNode l = dfs(i + 1, j, k - j);
        TreeNode r = dfs(i + 1 + k - j, k + 1, n - 1 - (k - j));
        return new TreeNode(v, l, r);
    }
}

C++

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        unordered_map<int, int> d;
        for (int i = 0; i < n; ++i) {
            d[inorder[i]] = i;
        }
        function<TreeNode*(int, int, int)> dfs = [&](int i, int j, int n) -> TreeNode* {
            if (n <= 0) {
                return nullptr;
            }
            int v = preorder[i];
            int k = d[v];
            TreeNode* l = dfs(i + 1, j, k - j);
            TreeNode* r = dfs(i + 1 + k - j, k + 1, n - 1 - (k - j));
            return new TreeNode(v, l, r);
        };
        return dfs(0, 0, n);
    }
};

TypeScript

function buildTree(preorder: number[], inorder: number[]): TreeNode | null {
    const d: Map<number, number> = new Map();
    const n = inorder.length;
    for (let i = 0; i < n; ++i) {
        d.set(inorder[i], i);
    }
    const dfs = (i: number, j: number, n: number): TreeNode | null => {
        if (n <= 0) {
            return null;
        }
        const v = preorder[i];
        const k = d.get(v)!;
        const l = dfs(i + 1, j, k - j);
        const r = dfs(i + 1 + k - j, k + 1, n - 1 - (k - j));
        return new TreeNode(v, l, r);
    };
    return dfs(0, 0, n);
}

Python

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        def dfs(i: int, j: int, n: int) -> Optional[TreeNode]:
            if n <= 0:
                return None
            v = preorder[i]
            k = d[v]
            l = dfs(i + 1, j, k - j)
            r = dfs(i + 1 + k - j, k + 1, n - k + j - 1)
            return TreeNode(v, l, r)

        d = {v: i for i, v in enumerate(inorder)}
        return dfs(0, 0, len(preorder))

如果题目中给定的节点值存在重复，那么我们只需要记录每个节点值出现的所有位置，然后递归构建出所有可能的二叉树即可。

Java

class Solution {
    private List<Integer> preorder;
    private Map<Integer, List<Integer>> d = new HashMap<>();

    public List<TreeNode> getBinaryTrees(List<Integer> preOrder, List<Integer> inOrder) {
        int n = preOrder.size();
        this.preorder = preOrder;
        for (int i = 0; i < n; ++i) {
            d.computeIfAbsent(inOrder.get(i), k -> new ArrayList<>()).add(i);
        }
        return dfs(0, 0, n);
    }

    private List<TreeNode> dfs(int i, int j, int n) {
        List<TreeNode> ans = new ArrayList<>();
        if (n <= 0) {
            ans.add(null);
            return ans;
        }
        int v = preorder.get(i);
        for (int k : d.get(v)) {
            if (k >= j && k < j + n) {
                for (TreeNode l : dfs(i + 1, j, k - j)) {
                    for (TreeNode r : dfs(i + 1 + k - j, k + 1, n - 1 - (k - j))) {
                        ans.add(new TreeNode(v, l, r));
                    }
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<TreeNode*> getBinaryTrees(vector<int>& preOrder, vector<int>& inOrder) {
        int n = inOrder.size();
        unordered_map<int, vector<int>> d;
        for (int i = 0; i < n; ++i) {
            d[inOrder[i]].push_back(i);
        }
        function<vector<TreeNode*>(int, int, int)> dfs = [&](int i, int j, int n) -> vector<TreeNode*> {
            vector<TreeNode*> ans;
            if (n <= 0) {
                ans.push_back(nullptr);
                return ans;
            }
            int v = preOrder[i];
            for (int k : d[v]) {
                if (k >= j && k < j + n) {
                    auto lefts = dfs(i + 1, j, k - j);
                    auto rights = dfs(i + 1 + k - j, k + 1, n - 1 - (k - j));
                    for (TreeNode* l : lefts) {
                        for (TreeNode* r : rights) {
                            TreeNode* node = new TreeNode(v);
                            node->left = l;
                            node->right = r;
                            ans.push_back(node);
                        }
                    }
                }
            }
            return ans;
        };
        return dfs(0, 0, n);
    }
};

Python

class Solution:
    def getBinaryTrees(self, preOrder: List[int], inOrder: List[int]) -> List[TreeNode]:
        def dfs(i: int, j: int, n: int) -> List[TreeNode]:
            if n <= 0:
                return [None]
            v = preOrder[i]
            ans = []
            for k in d[v]:
                if j <= k < j + n:
                    for l in dfs(i + 1, j, k - j):
                        for r in dfs(i + 1 + k - j, k + 1, n - 1 - (k - j)):
                            ans.append(TreeNode(v, l, r))
            return ans

        d = defaultdict(list)
        for i, x in enumerate(inOrder):
            d[x].append(i)
        return dfs(0, 0, len(preOrder))