64. 最小路径和

题目描述

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

 

示例 1：

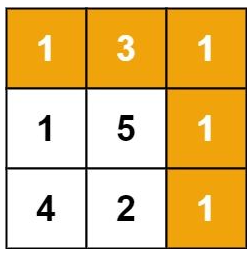
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

方法一：动态规划

我们定义 $f[i][j]$ 表示从左上角走到 $(i,j)$ 位置的最小路径和。初始时 $f[0][0]=grid[0][0]$，答案为 $f[m-1][n-1]$。

考虑 $f[i][j]$：

• 如果 $j=0$，那么 $f[i][j]=f[i-1][j]+grid[i][j]$；
• 如果 $i=0$，那么 $f[i][j]=f[i][j-1]+grid[i][j]$；
• 如果 $i>0$ 且 $j>0$，那么 $f[i][j]=min(f[i-1][j],f[i][j-1])+grid[i][j]$。

最后返回 $f[m-1][n-1]$ 即可。

时间复杂度 $O(m\times n)$，空间复杂度 $O(m\times n)$。其中 $m$ 和 $n$ 分别是网格的行数和列数。

Java

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[][] f = new int[m][n];
        f[0][0] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            f[i][0] = f[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            f[0][j] = f[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]) + grid[i][j];
            }
        }
        return f[m - 1][n - 1];
    }
}

C++

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int f[m][n];
        f[0][0] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            f[i][0] = f[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            f[0][j] = f[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j];
            }
        }
        return f[m - 1][n - 1];
    }
};

TypeScript

function minPathSum(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const f: number[][] = Array(m)
        .fill(0)
        .map(() => Array(n).fill(0));
    f[0][0] = grid[0][0];
    for (let i = 1; i < m; ++i) {
        f[i][0] = f[i - 1][0] + grid[i][0];
    }
    for (let j = 1; j < n; ++j) {
        f[0][j] = f[0][j - 1] + grid[0][j];
    }
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]) + grid[i][j];
        }
    }
    return f[m - 1][n - 1];
}

Python

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        f = [[0] * n for _ in range(m)]
        f[0][0] = grid[0][0]
        for i in range(1, m):
            f[i][0] = f[i - 1][0] + grid[i][0]
        for j in range(1, n):
            f[0][j] = f[0][j - 1] + grid[0][j]
        for i in range(1, m):
            for j in range(1, n):
                f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j]
        return f[-1][-1]